Approfondimento: modelli di ottmizzazione non lineare di Markowitz

I problemi di selezione del portafoglio (portfolio selection problems) rappresentano una classe molto importante e studiata, nell'ambito dell'ottimizzazione non lineare. Si tratta di modelli bi-criterio, che si prefiggono di determinare il portafoglio ideale, che vanti il miglior compromesso tra:

• elevato rendimento del portafoglio;
• ridotto rischio ad esso associato.

Siano:

• xj la frazione del portafoglio, espressa in percentuale, investita nell'asset j, j = 1, 2, ..., n;
• rj il rendimento medio dell'asset j, j = 1, 2, ..., n;
• σj la varianza osservata in corrispondenza dell'asset j, j = 1, 2, ..., n;
• R la soglia del rendimento del portafoglio;

si suppone che il portafoglio debba garantire un valore di rendimento atteso almeno pari ad R, minimizzando al contempo la varianza del portafoglio:

In alternativa, sia:

• V la soglia sulla varianza del portafoglio;

si può imporre che il portafoglio abbia un valore di varianza al di sotto della soglia V, volendo massimizzare il rendimento atteso:

Si tratta, in realtà, di due possibilità di risoluzione del problema bi-criterio, in ciascuna delle quali si vincola una della due quantità incognite (media o varianza), massimizzando o minimizzando la restante.

Indicando con:

• α il parametro di avversione al rischio, il quale quantifica l'importanza del rischio in relazione al rendimento;

 è possibile compattare le due espressioni, definendo il modello media-varianza:

Quanto più l'investitore sarà avverso al rischio, tanto più α sarà elevato; in forma matriciale, indicando con:

• x il vettore delle n percentuali di investimento;
• μ il vettore dei rendimenti medi osservati per gli n asset;
• Σ la matrice di varianze e covarianze relativa ai rendimenti osservati;

si avrà:

I modelli sopra riportati possono essere delle strategie di ottimizzazione mono-obiettivo volte ad individuare la frontiera efficiente, ovvero quella dei migliori compromessi.

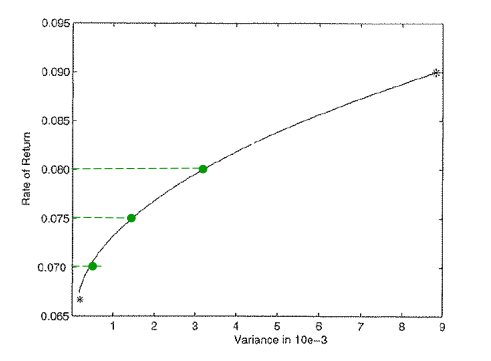
E' lecito a questo punto chiedersi come si possa, dati due punti collocati sulla frontiera efficiente, stabilire quale di essi sia associato alla situazione maggiormente desiderabile. In realtà, i due punti, nella figura riportata in basso x ed y, non sono confrontabili proprio perché appartenenti entrambi alla frontiera efficiente: semplicemente, rappresentano due compromessi diversi.

Se ci si limitasse ad ottimizzare un solo problema, non tenendo conto del vincolo sul restante, si otterrebbero i due estremi della frontiera.

Essendo la frontiera un insieme continuo di punti, corrispondenti a coppie di valori R e V, è possibile generare un'approssimazione di tale serie:

• stabilendo una serie di possibili valori per V, che rappresenta l'ascissa;
• risolvendo, per ciascuno di essi, il problema MM;

O, al contrario:

• stabilendo una serie possibili valori per R, collocato in ordinata;
• risolvendo, per ciascuno di questi valori, il problema MV.

(Fonte: dispense del corso "Metodi e modelli di ottimizzazione", prof.ssa Federica Ricca)