Nel 1990 tre economisti americani, William Shape, Merton Miller e Harry Markowitz, vincono il premio Nobel per l'Economia, «per i contributi pionieristici nell'ambito dell'economia finanziaria». Motivo del riconoscimento il capital asset pricing model (CAPM), modello matematico che descrive la relazione tra rendimento di un titolo e sua rischiosità.
Prima di procedere con la descrizione del modello, introduciamo alcuni aspetti preliminari, principalmente legati al quadro macroeconomico. Quando una società, una banca o uno Stato necessita di liquidità, ma ne è a corto, può decidere di cercare qualcuno, sia esso una azienda privata, una banca o uno Stato, disposto ad effettuare un prestito nei suoi confronti: a garantirlo vi sarà il titolo bancario. Parleremo di azioni laddove l'ente emittente sia un'impresa, pubblica o privata, mentre di obbligazioni nel caso in cui si tratti di una banca centrale, che operi quindi per conto di uno Stato. Ovviamente il prestito avviene purché, al termine di un periodo di tempo prestabilito, sia restituita non solo la somma di denaro ceduta, ma anche una quota di interessi: quest'ultima rappresenterà proprio il rendimento del titolo. Solitamente tassi di interessi maggiori corrispondono ad una minore affidabilità del soggetto che emette il titolo: più un ente economico sarà poco affidabile, più dovrà offrire tassi di interessi alti per i propri titoli, al fine di incentivare il loro acquisto. D'altro canto, più i tassi di interesse legati ai titoli emessi saranno elevati, maggiore sarà il rischio che il soggetto possa non restituire la quota dovuta al termine del periodo stabilito. Il rendimento è inoltre legato alla durata del titolo: mentre risulta più facile effettuare previsioni relative ai prossimi 6 o 12 mesi, maggiore incertezza è legata a quelle relative a periodi più ampi, con più alto rischio di default dell'ente, che renda impossibile la restituzione della cifra stabilita.
Nel capital asset pricing model si suppone che gli operatori finanziari operino secondo una logica di media-varianza, ossia:
- cercando di massimizzare il rendimento futuro atteso;
- cercando di minimizzare la varianza dei rendimenti, condizione che equivale a preferire soggetti economici.
L'ipotesi cardine del modello è che l'operatore finanziario basi la propria decisione riguardo l'acquisto di un titolo in base non solo al rendimento di questo, ma anche a quello del portafoglio, l'insieme di titoli che intende acquistare. Indicando quindi:
- con rf il rendimento lordo del titolo in questione, privo di rischio;
- con E[rp] il rendimento futuro atteso del portafoglio, ottenuto come somma, ponderata con pesi ωi, dei rendimenti che costituiscono un dato portafoglio:;
- con σp la deviazione standard dei rendimenti del portafoglio;
occorre massimizzare la funzione obiettivo:
Risolvendo il problema di ottimizzazione non lineare, in corrispondenza di un dato titoli i, la relazione ottenuta sarà:
avendo indicato con:
- ri il rendimento lordo del titolo in questione;
- rm quello relativo al portafoglio di mercato;
- rf il rendimento lordo del titolo in questione, privo di rischio;
- βim il rapporto tra la covarianza tra rendimento del titolo i-esimo e portafoglio e la varianza di quest'ultimo:
Il modello è utile:
- per valutare quanto le valutazioni di mercato si discostino dalle aspettative degli operatori: un'attività il cui prezzo sarà superiore al valore ottenuto con il capital asset pricing model risulterà sovraprezzata, una in cui sarà inferiore sottoprezzata;
- per valutare l'acquisto di un dato titolo, rispetto al mercato di riferimento: per βim maggiore di uno, il titolo i-esimo comporterà rischiosità maggiore, al contrario βim denoterà minore rischiosità;
- per βim maggiore di zero il trend dei due rendimenti sarà lo stesso (entrambi crescenti o decrescenti), risulterà opposto, invece, per βim minore di zero.
La difficoltà, di carattere puramente tecnico, risiede nel fatto che il coefficiente βim non può essere calcolato per via analitica, ma deve essere stimato. In questo contesto, la procedura più largamente adottata è una regressione a due passi.
Nel primo passo vengono stimati i coefficienti βim attraverso la serie storica equazioni lineari relative a dati istanti di tempo, chiamate modelli di mercato:
Nel secondo passo, le stime ottenute in precedenza vengono utilizzate come variabili esplicative attraverso cui stimare i rendimenti riferiti all'i-esimo titolo, sempre in un modello di regressione lineare, in un'ottica cross-section:
Se α risulterà pari al rendimento lordo privo di rischio, rf, e βim rappresenterà il premio per il rischio del portafoglio, allora il capital asset pricing model potrà essere adottato.
In realtà, il modello presuppone alcune ipotesi alquanto ristrettive:
- la concorrenza perfetta, secondo ciascun individuo può disporre di tutte le informazioni di cui necessiti, in qualsiasi momento;
- l'assenza di costi transazioni e tasse, che invece potrebbero frenare gli acquisti degli operatori finanziari;
- la supposizione di medesime aspettative degli operatori, senza tener conto della possibilità di un giudizio soggettivo.
Si tratta comunque di una innovativa proposta di strategia di trading, che ovviamente può essere adottata dall'investitore, sempre con la dovuta premessa che non sempre il mercato azionario riflette l'economia reale.
(Fonte: Wikipedia)
(Fonte: Wikipedia)

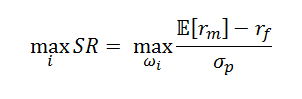




Nessun commento:
Posta un commento