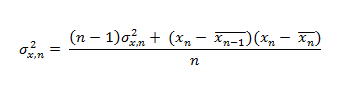E come altro iniziare un blog sulla statistica?
Qualsiasi analisi statistica non può prescindere dal calcolo della media; con questo termine viene indicato un singolo valore numerico che descrive sinteticamente un insieme di dati a disposizione. Esistono diverse tipologie di media; la più nota è indubbiamente la media aritmetica, calcolata come rapporto tra la somma e il numero delle osservazioni:
Qualora si avessero a disposizione dataset di grande entità, in cui si inseriscano costantemente nuovi dati, è ragionevole pensare di poter costruire un algoritmo iterativo ad hoc che permetta di calcolare il valore della media semplicemente aggiornando i valori precedentemente stimati, senza dover quindi calcolare somma e numero delle osservazioni ogni qual volta si inseriscano nuove rilevazioni. La formula utilizzata sarà:
Analogamente la varianza, definita come rapporto tra la somma degli scarti dalla media al quadrato e il numero delle osservazioni:
Potrà essere stimata come:
Se si hanno a disposizione più variabili, sarà anche possibile, per ciascuna coppia, calcolare la covarianza:
Stimata dall'algoritmo attraverso la formula:
I campi di applicazione di questi algoritmi, detti online algorithms, sono numerosi. Banalmente, consideriamo l'esempio di due studenti che vogliano calcolare la media dei propri esami universitari; si procede inizializzando le variabili Count (che rappresenterà il contatore del numero degli esami inseriti), MeanL e MeanK (rispettivamente, le medie calcolate ad ogni step e riferite a ciascuno dei due individui), PrevMeanL e PrevMeanK (le medie relative allo step precedente rispetto al corrente, necessarie per calcolare varianze e covarianza), VarL, VarK e Cov (le due varianze e la covarianza tra le due liste di dati) ed, infine, le due liste L e K, in cui successivamente verranno inserite le votazioni riportate per ciascun esame:
Public Class Form1
Private Sub Button1_Click(sender As Object, e As EventArgs) Handles Button1.Click
Dim Count As Integer
Dim MeanL As Double
Dim MeanK As Double
Dim PrevMeanL As Double
Dim PrevMeanK As Double
Dim VarL As Double
Dim VarK As Double
Dim Cov As Double
Dim L As New List(Of Integer)
Dim K As New List(Of Integer)
L.Add(30)
L.Add(29)
L.Add(28)
L.Add(28)
L.Add(28)
L.Add(27)
L.Add(30)
K.Add(23)
K.Add(29)
K.Add(30)
K.Add(30)
K.Add(25)
K.Add(18)
K.Add(27)
A questo punto è possibile inserire le formule precedenti all'interno del ciclo iterativo:
For i As Integer = 0 To L.Count - 1
PrevMeanL = MeanL
PrevMeanK = MeanK
Count = Count + 1
MeanL = ((Count-1)*MeanL+L(i))/Count
MeanK = ((Count-1)*MeanK+K(i))/Count
VarL = ((Count-1)*VarL+(L(i)-PrevMeanL)*(L(i)-MeanL))/Count
VarK = ((Count-1)*VarK+(K(i)-PrevMeanK)*(K(i)-MeanK))/Count
Cov = ((Count-1)*Cov+(L(i)-PrevMeanL)*(K(i)*MeanK))/Count
In Visual Basic è possibile creare un bottone e far sì che, cliccandovi sopra, compaiano all'interno di una casella di testo i valori delle statistiche descrittive che ci occorrono, ottenuti in corrispondenza di ciascuno step; a tale scopo, è sufficiente inserire i comandi precedenti nel gestore dell'evento relativo al bottone, imponendo infine l'apparizione dei valori di interesse nella casella di testo:
RichTextBox1.AppendText(MeanL.ToString("#.##") & (" ") & MeanK.ToString("#.##")&(" ")&VarL.ToString("#.##")&(" ")&VarK.ToString("#.##")&(" ")&Cov.ToString("#.##")&vbCrLf)
Next
End Sub
End Class
Gli online algorithms riescono a risolvere molti problemi computazionali che si presentano laddove viene applicato il calcolo "tradizionale" della media, quali ad esempio la cosiddetta catastrophic cancellation. Si tratta di un problema strettamente legato alle approssimazioni effettuate dal software, per cui due valori irrazionali che presentano le prime cifre immediatamente successive alla virgola uguali vengono approssimati alla medesima quantità; dunque effettuando al differenza tra questi ultimi, il risultato potrebbe essere stimato zero, pur trattandosi di un valore non nullo. Considerando, ad esempio:
1.32654965378745623385885
e
1.3265496537
se il software riesce solo ad approssimare alla decima cifra decimale, la differenza, pur risultando:
1.32654965378745623385885 - 1.3265496537 =0.00000000008745623385885
sarà riportata come nulla. Tale effetto viene spesso identificato col termine loss of significance.
(Fonte: Wikipedia)
(Fonte: Wikipedia)